
The relationship between the current and voltage in a circuit was studied and formulated into laws by Gustov Kirchhoff, a German Physicist in 1845. Kirchhoff’s laws state the relationship between current and voltage in an electric circuit. They are applicable for both AC and DC circuits and forms the basis for circuit analysis.
Kirchhoff’s laws
Kirchhoff’s laws are classified into:
- Kirchhoff’s current law
- Kirchhoff’s voltage law
Kirchhoff’s current law
Kirchhoff’s current law states that the algebraic sum of all the current flowing to a node and out of the node in a circuit is zero.
Simply, the algebraic sum of currents at the meeting point of two or more conductors is zero. Node is nothing but the junction of two or more conductors.

Let us understand this with pipeline analogy. Consider that you have connected three hoses to a tee connector. One of the hoses is connected to a pump and the other two are connected to water the plants in your garden. Kirchhoff’s current law, when applied to this example, states that the amount of water entering the tee connector is equal to that leaving out from it to the garden.
Consider a circuit as shown:
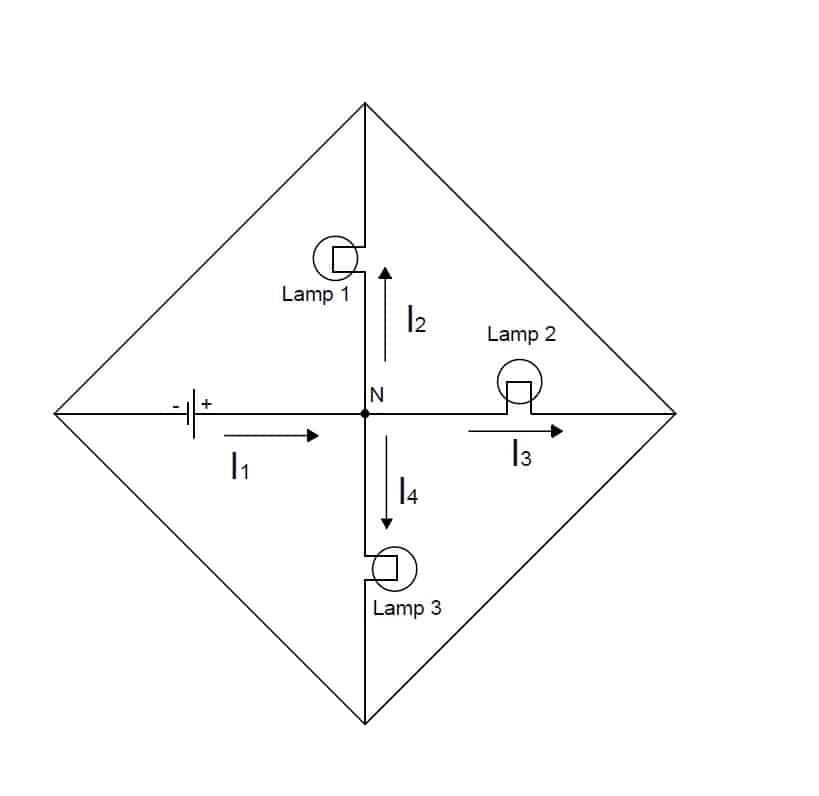
According to Kirchhoff’s current law, the sum of currents flowing towards the node N (I1) IS equal to the sum of current flowing away from the node (I2, I3, I4).
I1 = I2 + I3 + I4
I1 – I2 – I3 – I4 = 0
The mathematical expression of Kirchhoff’s law is
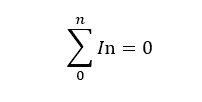
Kirchhoff’s current law is commonly known as Kirchhoff’s first law.
Kirchhoff’s voltage law
A circuit is a closed path of current flow. It consists of a power source and other circuit components. Every component has a power loss across it. The voltage drop across each circuit component differs in accordance to its resistance or impedance. Kirchhoff’s law relates these voltage drops to the source voltage.
According to Kirchhoff’s voltage law, the algebraic sum of voltages around a closed loop is always zero.
Let us consider the following circuit.
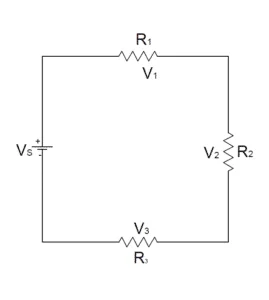
The above circuit consists of four components:
- The voltage source is 20V.
- A resistor R1 of 10ohms.
- Two resistors R2 and R3 of 5ohms.
The equivalent resistance offered by the circuit to the power source is
Req = 10 + 5 + 5 = 20 ohm
Total current flow = 20V / 20 ohm = 1A.
Now calculate the voltage drop across each resistor.
Voltage drop across resistor R1, V1 = 10 x 1 = 10V
Voltage drop across resistor R2, V2 = 5 x 1 = 5V
Voltage drop across resistor R3, V3 = 5 x 1 = 5V
Total voltage drop = V2 + V2 + V3 = 10 + 5 + 5 = 20V
Hence, V1 + V2 + V3 = Vs, V1 + V2 + V3 – Vs = 0
This is what Kirchhoff’s voltage law states.
Application of Kirchhoff’s laws
Using Kirchhoff’s current law, current flow in various branches of a node can be easily calculated. We should be careful while considering signs of quantities of currents. The current flowing towards the node is considered positive and the current flowing away from the node is considered negative. Kirchhoff’s voltage law is used in circuit analysis to calculate unknown voltages, resistance and currents in a loop.
Excellent explanations.. thanks
Good, well explained