Thevenin’s and Norton’s theorems are circuit simplification methods, applied to simplify complex linear circuits and making circuit analysis easy and fast. These theorems are proposed by Léon Charles Thévenin and E. L. Norton respectively. We can convert a Thevenin’s equivalent circuit to Norton’s and vice versa.
Thevenin’s theorem
Thevenin’s theorem states that any linear network with several power sources, resistances and a variable load can be represented in a much simpler circuit containing a single voltage source (VTH) in series with a resistance (RTH) and the variable load, where VTH is the open-circuit voltage at the terminals of the load and RTH is the equivalent resistance measured across the terminals while independent sources are turned off.
Norton’s theorem
Norton’s theorem states that a linear two-terminal circuit can be replaced by an equivalent circuit consisting of a current source IN in parallel with a resistor RN, where IN is the short-circuit current through the terminals and RN is the input or equivalent resistance at the terminals when the independent sources are turned off.
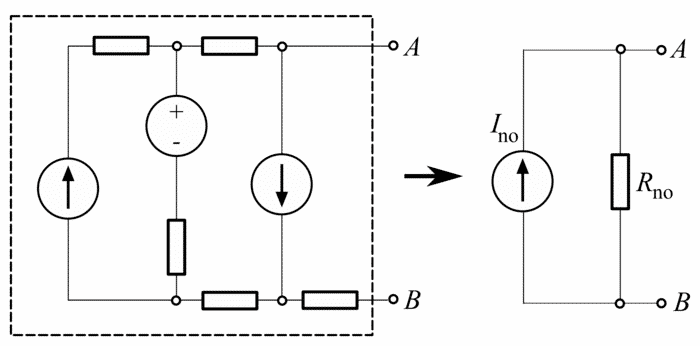
Convert Thevenin’s equivalent to Norton’s equivalent circuit
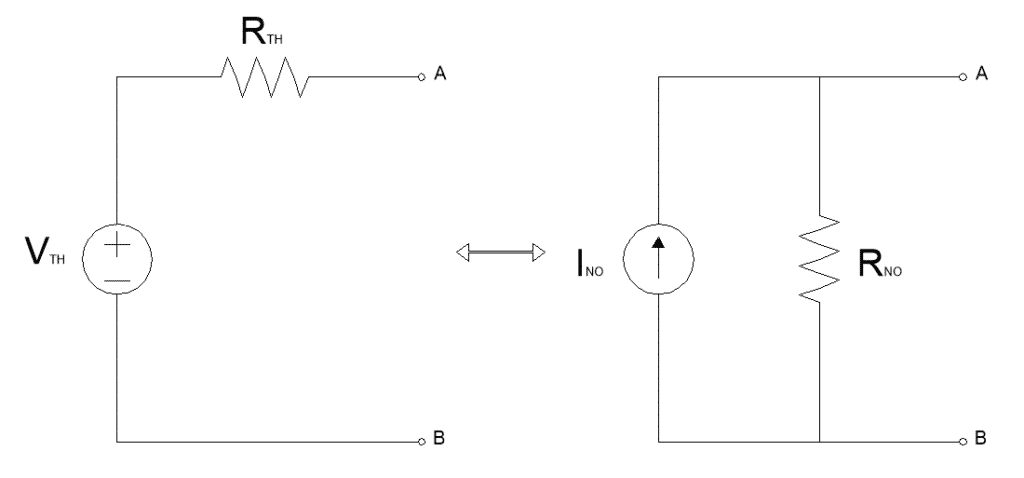
Thevenin’s equivalent to Norton’s equivalent circuit by applying ohm’s law.
According to Ohm’s law: V=I.R
As we know, RTH = RNO
Therefore, all we need to do is find the Current source. Applying the Ohm’s law:
INO = VTH/RNO
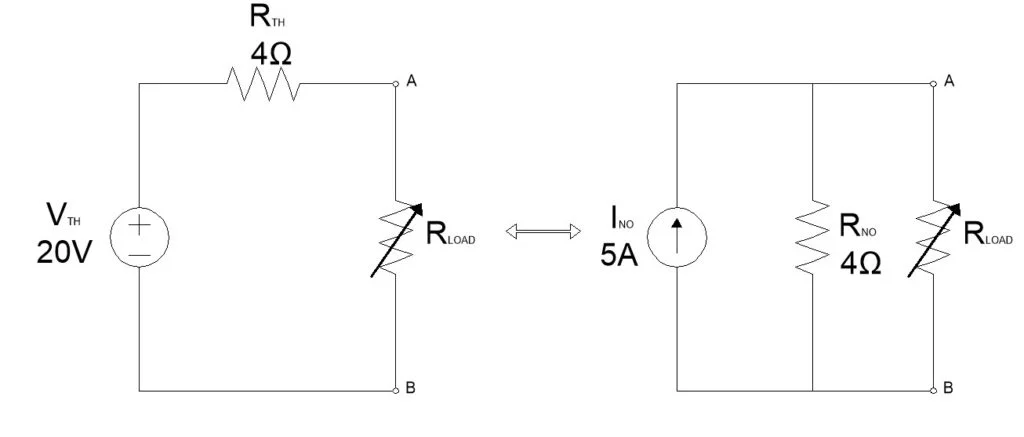
Example
Let’s find Norton’s equivalent for the following Thevenin’s equivalent circuit.
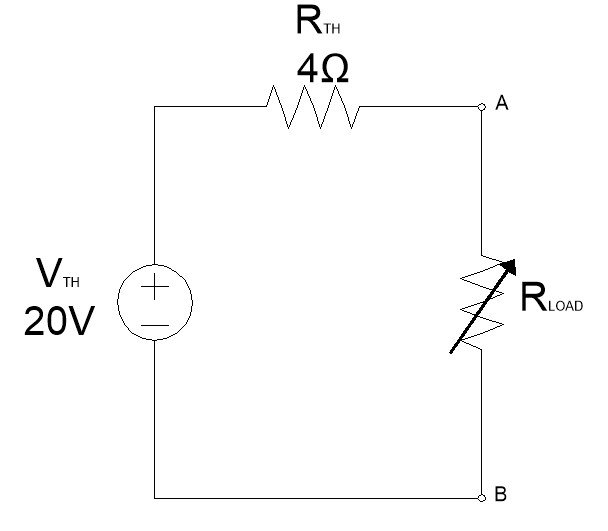
Norton’s current source INO = VTH/RNO = 20/4 = 5A
Norton’s equivalent circuit is as follows: