Superposition theorem

Superposition theorem can be used to find the current or voltage in any circuit containing more than one independent sources. By using this method, we calculate the contribution of each independent source and sum them up. Superposition is not limited to circuit analysis but is applicable in many fields where cause and effect bear a linear relationship to one another.

Superposition theorem statement

Superposition theorem states: “In any network containing more than one power source, the resultant current and voltage in any branch can be found by considering each source separately and adding up their effects, all other sources being replaced at that time by their respective internal impedances.”

Every source in the circuit affects the current flow and voltage across each circuit elements. In order to calculate the contribution of each circuit source independently, remove all other sources but one and replace the voltage source with a short circuit and replace current sources with open circuit. While replacing, the internal resistances of the sources remain in the circuit. By this way calculate the effect of each source on the circuit elements.

Example for source replacement.

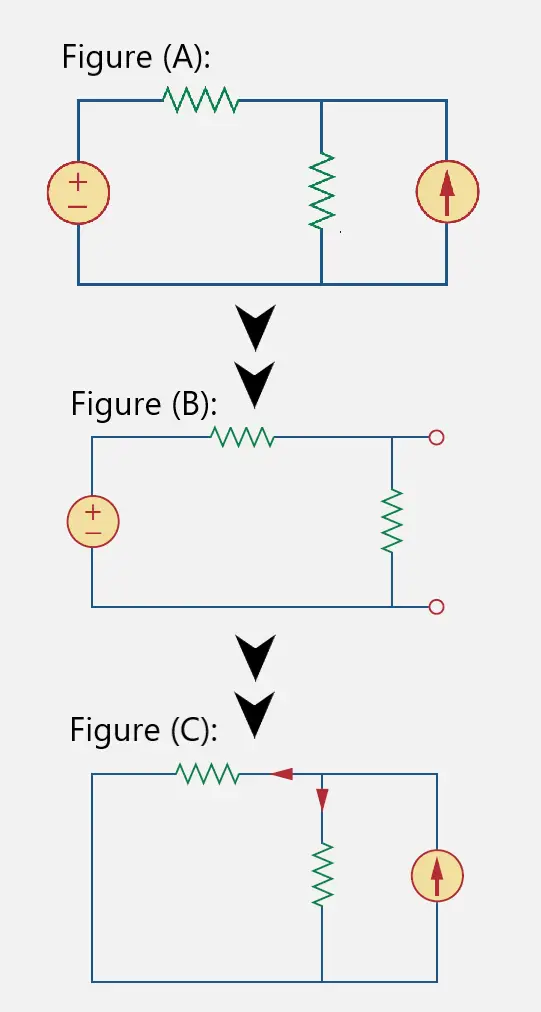
Figure (A) shows the actual circuit, Figure (B) shows the replacement of current source with an open circuit and Figure (C) shows the replacement of voltage source with short circuit.

After calculating the contributions of each element, sum up the results to find the resultant current or voltage in each branch of the circuit. When you sum the contributions from the sources, the signs of each parameter should be taken into consideration. The algebraic sum of contributions of each source gives the resultant current or voltage.

Steps to solve networks using Superposition theorem

1. Turn off all independent sources but one. (Short circuit the voltage sources and open circuit the current sources).
2. Find the output (voltage or current) due to that active source using mesh or nodal analysis.
3. Repeat steps 1 and 2 for each of the other independent sources.
4. Finally, algebraically add the contributions due to the independent sources, to calculate the total contribution by all the sources.

Examples:

Let’s solve the following circuit and find the current ‘i ’ using superposition theorem. We will follow the above steps.

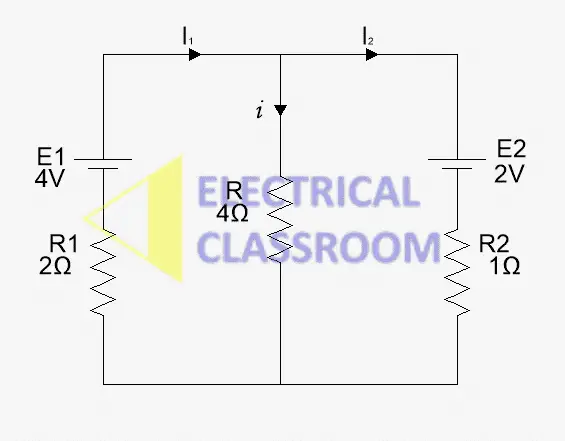
Step 1:

Turn off all independent sources but one. (Short circuit the voltage sources and open circuit the current sources).

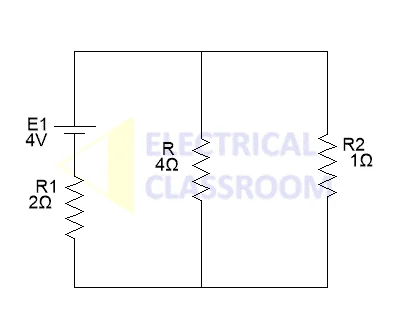
Step 2:

Find the output (voltage or current) due to that active source using mesh or nodal analysis.

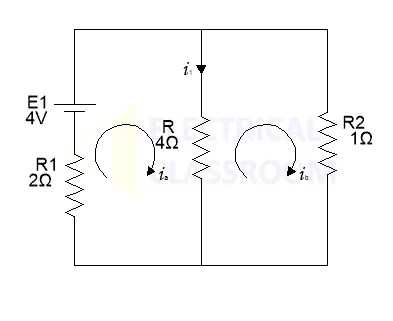
Using mesh analysis:

2.i_a + 4.( i_a – i_b)– 4  = 0 ; 4.( i_a – i_b) + i_b = 0

Solving the above equations, we get:

i_a = 1.429 A

i_b = 1.143 A

i₁ = i_a – i_b = 0.286A

Step 3:

Repeat Step-1 and Step-2, but this time we analyze the circuit with E₁ source shorted and taking E₂ into consideration.

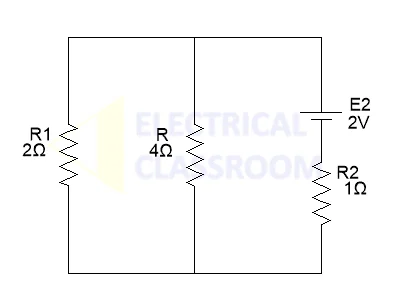
Let us analyze the above circuit using mesh analysis method:

Using mesh analysis:

2.i_c + 4.( i_c – i_d) = 0 ; 4.( i_d – i_c) + i_d – 2 = 0

Solving the above equations, we get:

i_c = 0.571 A

i_d = 0.857 A

i₂ = i_d – i_c = 0.286A

Step 4:

Algebraically add the individual contributions of each source to find I₁,I₂ & i.

I₁ = i_a – i_c = 1.429 – 0.571 = 0.858A

I₂ = i_d – i_b = 1.143 – 0.857 = 0.286A

i = i₁ – i₂ = 0.286 +0.286 = 0.572A

Drawbacks of superposition theorem

Superposition Theorem may involve more work if there are many sources. Power dissipation cannot be calculated using this theorem. It can be applied for the calculation of current and voltage only. Being a non-linear function, power dissipation, do not algebraically add to an accurate total when only one source is considered at a time.