In an electric circuit, power flows from the source to the load. The source itself has some amount of impedance which affects the current flow. Therefore, transfer of power depends not only on the load impedance but also the source impedance. Maximum power transfer theorem speaks about the relationship between the source impedance, load impedance and the power flow from the source to the load.
Maximum power transfer theorem – Statement
The power transferred from a supply source to a load is at its maximum when the resistance of the load is equal to the internal resistance of the source.
Note: This theorem lets us improve power transfer in a circuit, but not circuit efficiency.
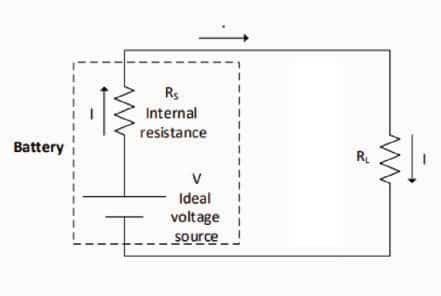
Explanation
The above circuit shows a battery with an EMF V, internal resistance Rs and a load resistance RL. According to maximum power transfer theorem, maximum power flows to RL when RS = RL. This theorem helps us choose the load resistance when we have a source with a known internal resistance.
Verification of theorem
Let us verify the theorem with an example.
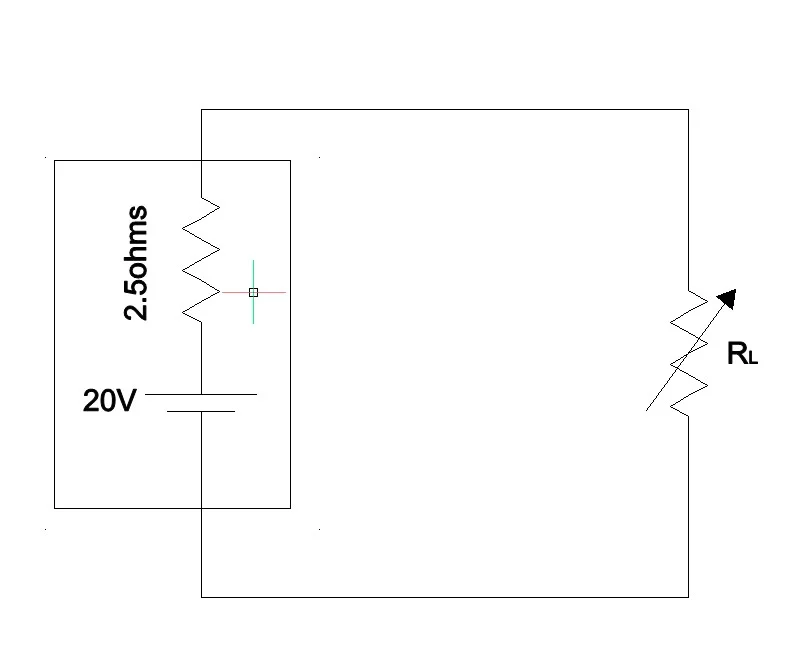
For the above circuit calculate the maximum power that can be transferred from the source. Let us vary the load resistance from 0 to 5 in steps of 0.5 and find out at which point the power transferred is maximum.
When RL = 0 ohm,
Total circuit resistance = 2.5 + 0 = 2.5 Ohms
Current flow to the Load = 20V/2.5 = 8A
Power delivered to the load = I2R = 82x 0 = 0 watts
When RL = 0.5 ohm,
Total circuit resistance = 2.5 + 0.5 = 3 Ohms
Current flow to the Load = 20V/3 = 6.67A
Power delivered to the load = I2R = 6.672x 0.5 = 21.125 watts
When RL = 1 ohm,
Total circuit resistance = 2.5 + 1 = 3.5 Ohms
Current flow to the Load = 20V/3.5 = 5.71A
Power delivered to the load = I2R = 5.712x 1 = 32.6 watts
Similarly lets calculate the power delivered for other values of load and tabulate it below:
| Load Resistance | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 |
| Power delivered | 0 | 22.22 | 32.65 | 37.5 | 39.5 | 40 | 39.67 | 38.89 | 37.87 | 36.73 | 35.56 |
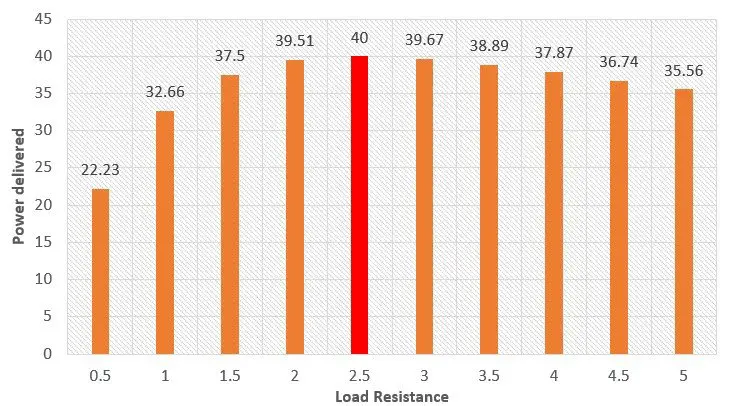
From the above table we can notice that the power delivered is maximum at 2.5 ohm which is equal to the source resistance. This verifies maximum power transfer theorem.
Misconception
The theorem tells us to choose the load resistance when we have a source with a known internal resistance. It is a common misconception to apply the theorem in the opposite scenario. It does not say how to choose the source resistance for given load resistance. The power transfer maximizes when the internal resistance of the source zero, regardless of the load resistance.
