As we know, in a parallel circuit current divides into all branches. The current flow through each branch is inversely proportional to the resistance offered by each one them. The branch having higher resistance allows lesser current and the branch having lesser resistance allows more current. Current division rule is applied while finding current flow through each branch of the circuit.
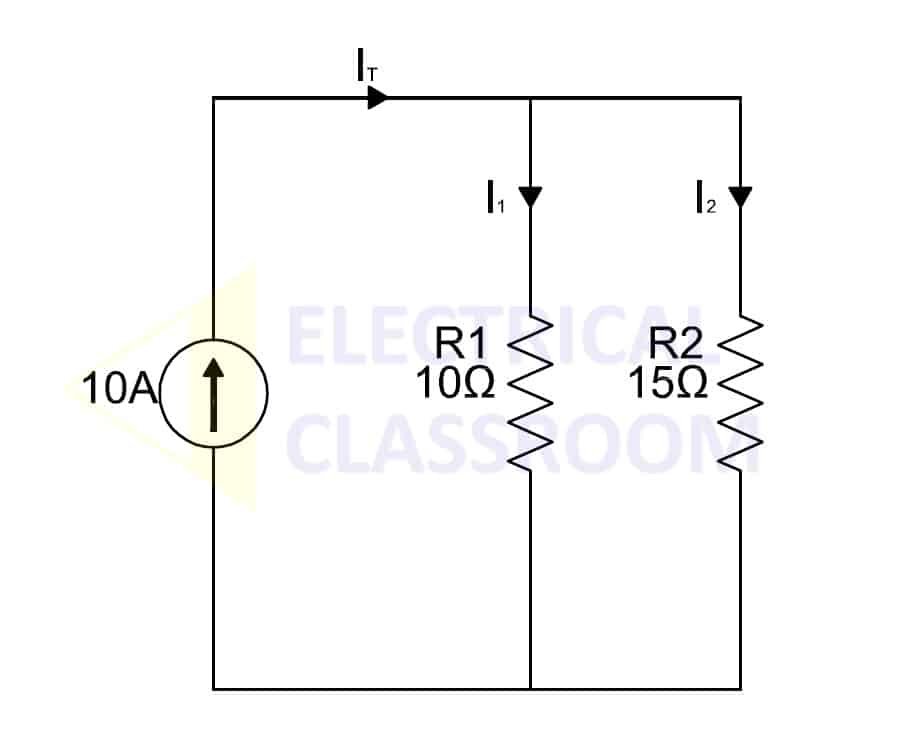
Let us consider the above circuit in which two resistors connected in parallel. The current, IT, from the source divides into I1 and I2 and passes through the resistors R1 and R2.
IT = I1 + I2
The current through each resistor can be calculated using current division rule. According to the current division rule, the current through any branch is equal to the ratio of the total resistance in parallel to the branch to the total resistance, multiplied by the total current in the circuit.
Applying current division rule in the above circuit,
Current flow through R1, I1 = IT . R2/(R1+R2)
Current flow through R2, I2 = IT . R1/(R1+R2)
For the above circuit,
I1 = 10 x 15/25 = 6A
I2 = 10 x 10/25 = 4A
In general, current flow in nth branch of a circuit containing m branches can be determined by
![\[I_n = I_T . \frac{R_T}{R_T + R_n}\]](https://www.electricalclassroom.com/wp-content/ql-cache/quicklatex.com-a91ed863c23ea2158094c0611065d074_l3.svg "Rendered by QuickLaTeX.com")
Where,
In – Current flow in nth branch of the circuit.
IT – Total current flow entering the circuit.
RT – Total resistance in parallel to the nth branch.
Rn – resistance in the nth branch.
Example for Current division rule:
Calculate the current flow in each branch of the circuit shown below:
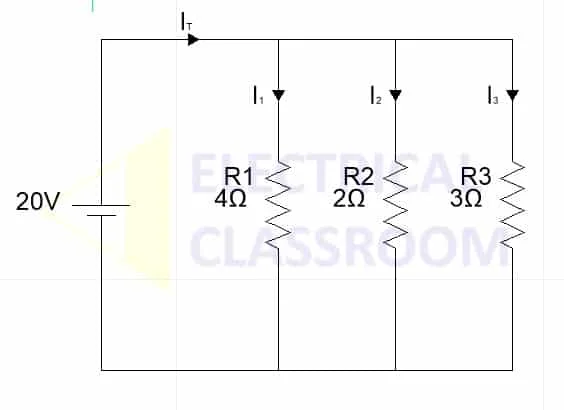
Equivalent resistance of the circuit ,
Equivalent resistance =
![\[\frac{3 X 4}{3+6+4} = 0.925 \Omega\]](https://www.electricalclassroom.com/wp-content/ql-cache/quicklatex.com-ce3f8eba79cc48aea065d20f894dcf72_l3.svg "Rendered by QuickLaTeX.com")
Total current IT = 20 / 0.925 = 21.62 A
To find the current through R1,
Total resistance in parallel to R1 = 2×3 / 2+3 = 1.2Ω
![\[I_1 = 21.62 X \frac{1.2}{4 + 1.2} = 4.99 A\]](https://www.electricalclassroom.com/wp-content/ql-cache/quicklatex.com-fca4b23a5527abeb296e5fbeaa1eef30_l3.svg "Rendered by QuickLaTeX.com")
To find the current through R2,
Total resistance in parallel to R2 = 4×3 / 4+3 = 1.72 Ω
![\[I_2 = 21.62 X \frac{1.72}{2 + 1.72} = 9.99 A\]](https://www.electricalclassroom.com/wp-content/ql-cache/quicklatex.com-05005a1c88311d7925da520e067521c4_l3.svg "Rendered by QuickLaTeX.com")
To find the current through R3,
Total resistance in parallel to R3 = 4×2 / 4+2 = 1.33 Ω
![\[I_3 = 21.62 X \frac{1.33}{3 + 1.33} = 6.64 A\]](https://www.electricalclassroom.com/wp-content/ql-cache/quicklatex.com-492b7779567defa33cdd9d0d6cfed82f_l3.svg "Rendered by QuickLaTeX.com")
Similarly, the current through any branch of resistors in a circuit can be calculated using current division rule.
Excellent explanation of what a current divider is and how to do the calculations. Even though I have a BS in Physics, I finally look at a circuit, recognize it is a current divider and can calculate the currents.
Great explanation