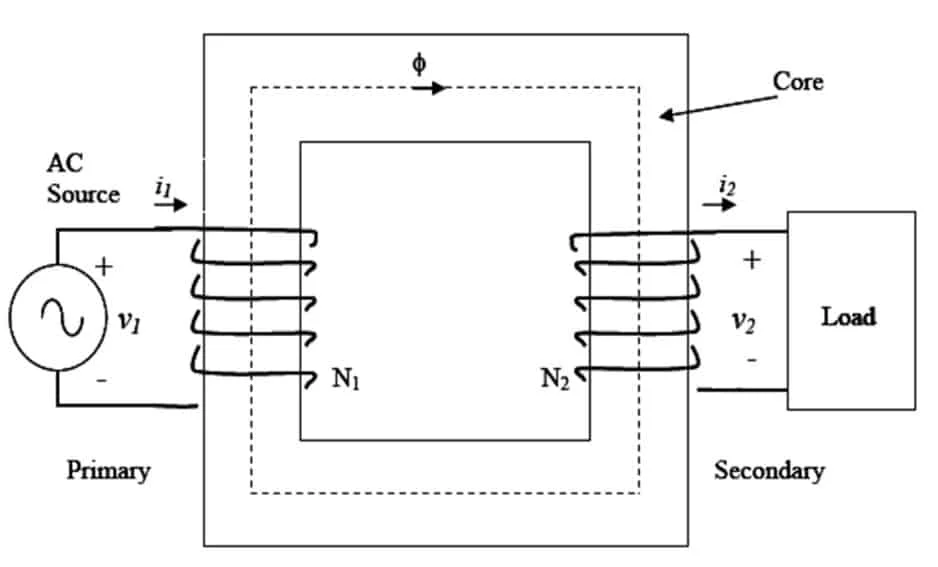
EMF equation of transformers

EMF equation of transformers lets you calculate the RMS values of induced voltages in the primary and secondary windings of a transformer. An alternating voltage, when applied to the primary of a transformer, produces an alternating magnetic field which induces EMF in the secondary windings.

EMF equation of transformers explained

The produced magnetic flux is alternating in nature and lags the applied voltage by 900. However, the flux remains in phase to the magnetizing current. The instantaneous value of flux is given by

    \[ \phi (t) = \phi_{max}Sin \omega t \]

Where, φmax is the maximum value of flux produced and ωt is the time period.

The instantaneous value of the applied voltage is given by

    \[ v_1 = V_{max}Sin (\omega t + \frac {\pi}{2}}) \]

Where, v1 is the applied voltage and ‘+π/2’ indicates that the voltage leads the flux.

If N1 and N2 are the numbers of primary and secondary turns, the EMF inducing in the primary and secondary winding are given by:

    \[ e_1 = -N_1 \frac {d\pi}{dt} \]

    \[ e_1 = -N_1 \frac {d (\phi_{max}Sin \omega t)}{dt} = -N_1 \phi_{max} \frac {d (Sin 2\pi f t)}{dt} \]

    \[ \frac {d (Sin 2\pi f t)}{dt} = 2 \pi F cos 2\pi = 2 \pi f \]

Therefore

    \[ e_1 = 2 \pi f N_1 \times \phi_{max} = 4.44 N_1 \times \phi_{max} f \]

Similarly,

    \[ e_2 = 2 \pi f N_2 \times \phi_{max} = 4.44 N_1 \times \phi_{max} f \]

e1 and e2 are the EMF equations of primary and secondary coils of a transformer. In general, the EMF equation of transformers is as follows:

    \[ E = 2 \pi f N_2 \times \phi_{max} = 4.44 N_1 \times \phi_{max} f \]

Voltage transformation ratio of a transformer

Voltage transformation ratio of a transformer is the ratio of primary and secondary voltages.

    \[ Voltage \mspace{6mu} transformation \mspace{6mu} ratio = \frac{V_1}{V_2} =\frac {4.44 N_1 \times \phi_{max} f }{4.44 N_2 \times \phi_{max} f } \]

    \[ \frac{V_1}{V_2} = \frac{N_1}{N_2} \]

Leave a Reply