Inductance
A conductor carrying current produces a magnetic field around it. This magnetic field follows a circular path. When the same conductor is wound over a cylindrical solid core, the magnetic field formed around it amplifies. Any change in the rate of current flow through this conductor causes a change in the magnetic field, thereby inducing voltage and opposing the flow of current through it. This property of a coil is called inductance.

Definition
Inductance can be defined as the property of any coil to store energy, induce voltage and oppose the current flow through it. It is represented by the letter L and the coil is known as an inductor.
Inductor
An inductor is a two-terminal device passive element that can store energy in the magnetic field. The inductance of an inductor depends on its physical properties and can be calculated using the following formula.
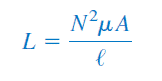
Where N is the number of turns of the coil, µ is its permeability, A is the area of cross-section and l is the length. Therefore, the inductance of an inductor increases with an increase in the number of turns and its area of cross-section and reduces by the increase in its length.
Unit of Inductance
Inductance is measured in henry (H), after an American physicist Joseph Henry. An inductor is said to have an inductance of one henry if an EMF of one volt is induced in it when the current varies uniformly at the rate of one ampere per second.
Voltage-current relationship
According to Ohm’s law, the voltage drop across a device is given by V=IR. Where R is a proportionality constant. In the case of an inductor, this R turns to be L (inductance). Consider that the current flowing through the coil changes from i1 to i2 in a time t. The voltage induced across the inductor is given by the following equation:
v = L. (i1 – i2 )/ t
v = L. di/dt
This equation says that the voltage across the inductor is proportional to the rate of change of current flowing through it. Practically the voltage across an inductor cannot change instantaneously because the inductor opposed the change in current through it. But the voltage across it can change abruptly.
Properties of an inductor
From the above equation, we can conclude that voltage across an inductor is zero when the current flowing through it is constant (di/dt = 0). Hence an inductor acts as a short circuit for dc when the rate of change of current through it is constant. Also current through an inductor cannot change instantaneously. An ideal inductor should never dissipate the stored energy. But practically it loses the stored
Self-Inductance
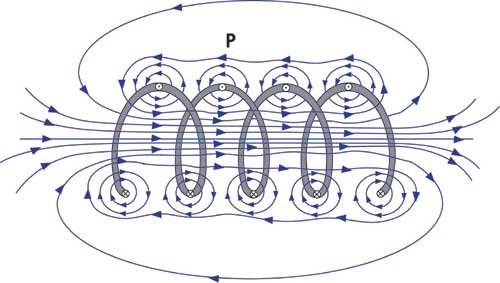
Self-inductance is a property of an inductor to induce voltage to itself whenever there is variation in the current flowing through it. Voltage is induced in such a way to oppose the flow of current through it and this process of an inductor to oppose the current flow through itself is known as self-induction.
Mutual Inductance
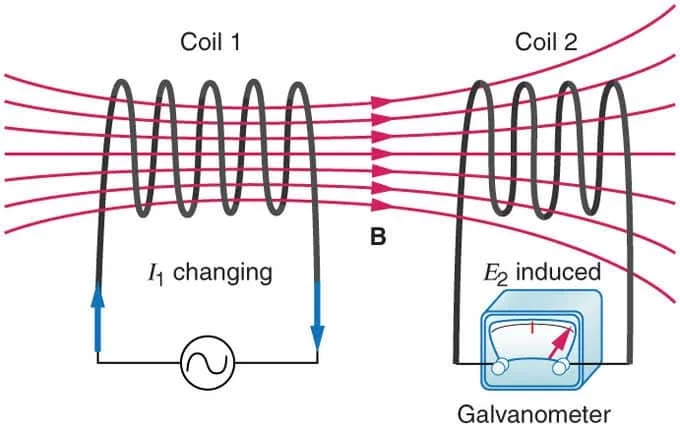
Mutual inductance is the property of an inductor to induce a voltage in another close to it. This happens when the magnetic field generated by the first coil that carries a time-varying current through it crosses the other coil. The process of mutual inductance is known as mutual induction.