Today most of the electric loads work on AC power. Every electric load possess a certain amount of resistance. Some loads, in addition to resistance, possess capacitance or inductance. The total impedance offered by the load to the current flow determines how much active and reactive power it would consume. The concepts of active power, reactive power and apparent powers may be a little tricky to understand. The below content can help you understand them.
Active power or Real power
Active power is the actual power dissipated or consumed by an electric load. It depends on the total load impedance. Active power is also known as True power and Real power. It is measured in Watts. Active power is denoted by the letter P.
Active power does not produce any phase shift between current and voltage. Hence current and voltage are always in phase for a resistive load.
Reactive power
Reactive power can be defined as an imaginary power in a capacitive or inductive load. It is measured in VAR (Volt ampere reactance) and denoted by the letter Q.
Reactive power can a little tricky to understand. This exists in the system when the voltage and current in an AC circuit are not in phase. Passive devices such as capacitors and inductors do not actually dissipate power, in turn, stores it in the form of electric charges or magnetic field. This stored energy can be revived from the devices later. Hence it is a form of energy that is neither lost nor gain yet affect the system performance. Even though capacitive and inductive loads do not dissipate power, it causes unwanted voltage dips and current flow in the system.
The rate at which active power and reactive power are consumed by the load is determined by the power factor of the load.
Complex and apparent power
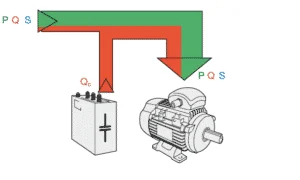
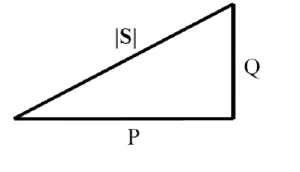
Complex power is the complex sum of real and reactive powers. Apparent power is the absolute value of complex power. It is a calculated value of power, that is independent of the type of load. It is measured in VA (volt-ampere). Apparent power is denoted by the letter S. It is similar to power in a DC circuit i.e. the arithmetic product of voltage and current.
Calculation of Active, Reactive, Apparent, and complex powers.
Let us consider a simple circuit with resistance R, Reactance X and impedance Z. Let V be the applied voltage and I be the current flow in the circuit.
Active power or Real power or True power completely depends on circuit resistance in a purely resistive load. Hence active power can be expressed as follows.
Active power, P = (Current)2 x Resistance = I2R
If the circuit is a purely reactive circuit (resistance=0), active power shall be zero. Reactive power in a purely reactive circuit can be calculated using the following formula:
Reactive power, Q = (Current)2 x Reactance = I2X
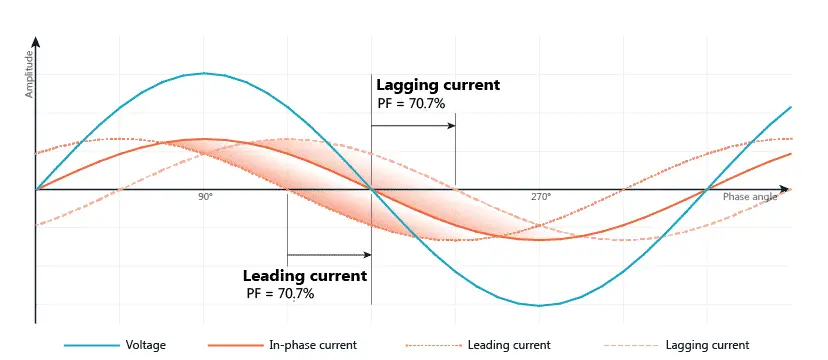
In a purely reactive circuit, the current leads the voltage or lags it depending on the type of reactance (inductive or capacitive). In an AC circuit having both resistive and reactive components, the power consumed can be calculated using the following formula:
Active power, P = VI.CosΦ
Reactive Power, Q = VI.SinΦ
Complex Power S = VI.CosΦ + j.VI.SinΦ
Apparent power, |S| = VI = I2Z
Where Z is the total impedance offered by the circuit to the current flow and Φ is the phase shift between current and voltage.
WELL EXPLAINED