As we know the current is the flow of free electrons through material from a higher potential to a lower potential. During this flow, few of these electrons collide with other atoms in the material and lose their energy in the form of heat. These collisions cause a drop in potential across the material. This property of a material to oppose the flow of current through it is known as resistance. The amount of resistance produced by a material to the current flow depends on the number of free electrons present in it and the types of obstacles present in it.

Definition of resistance
The property of a material to resist the free flow of electrons through it is called resistance. It is denoted by R. Resistance of a material depends on its cross-sectional, length and it’s relative permeability.
The resistance of a material is given by R = ρ l/A
where ρ is the relative permeability of the material, l is the length of the material and A is its cross-sectional area.
Symbol of resistance:
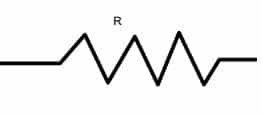
Unit of resistance:
The unit of resistance is ohm and the unit of resistance is symbolically represented by the Greek letter Ω. One Ohm is the amount of resistance that would limit the current flow through a conductor to 1 ampere when a 1 volt is applied across it.
Ohm’s law:
According to ohm’s law, the current flowing through a resistance is directly proportional to the voltage across it.
V = IR
R= V / I
V– Voltage across the resistor
I – Current flowing through it.
When current flows through a conductor few electrons lose their energy due to collision with the atoms in it. The energy lost due to collision is dissipated in the form of heat. The amount of current flow through a conductor is inversely proportional to its resistance. Higher the resistance lower will be the current flow.
Resistor
A resistor is a two-terminal device which is used in an electric circuit and provides predefined resistance to the flow of current in the circuit. The resistance of a resistor can be linear or non-linear depending on the material used. The resistance of a linear resistor is independent of the applied voltage. But the resistance of a non-linear resistor varies upon the applied voltage. Resistors made of semi-conductor are non-linear.
Power absorbed by the resistor
The power absorbed by the resistance is
P=VI = I (IR) = I2R
Where V is the voltage across the resistor and I is the current flowing through it.
The energy lost across a resistor
The energy lost across a resistor in a time t is given by
E= (V2 / R) t = I2Rt
“V” is the voltage across the resistor, “I” is the current flowing through it and “t” is a time in seconds.
Temperature coefficient of resistance
The resistance of any material is temperature-dependent. It increases with increase in temperature for metals. But resistance is inversely proportional to temperature for semiconductors. The resistivity of a semiconductor decreases with an increase in temperature.
Problems based on resistance.
Problem 1:
A 20-ohm resistance is connected across a 12V battery. Calculate the power loss and the energy loss in the circuit when it is kept closed for 3 minutes.
Solution:
Current flowing though the resistor R= V / I = 12/20 = 0.6A
Power lost across the resistor, P = I2R = 0.62 x 20 = 7.2 Watts
Energy lost in the resistor, W= I2R x t = 7.2 x 3x 60s = 1296 Joules
Problem 2
If a resistance connected across a 6V battery allows a current of 0.2 ampere through it, find the value of resistance.
Solution :
According to ohm’s law, R= V / I = 6/0.2 = 30 ohms.
Resistance connected in series.
In a series circuit current through all the elements is equal. Let V1, V2, V3, … Vn is the voltage across each resistance. Then total voltage across the series-connected resistance is given by
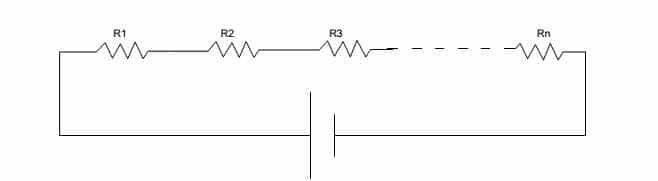
Vs = V1 + V2 + V3 + … VnIReq = IR1 + IR2+ IR3 + …..+ IRn
Dividing the whole equation by I, Req = R1 + R2+ R3 + …..+ Rn
From the above equation it is evident that in a series connection of resistances, the total resistance is equal to the sum of the individual resistances.
Resistance connected in parallel.
In a parallel circuit voltage across every branch is equal. Let I1, I2, I3, … In is the current across each resistance. Then total current across the parallel-connected resistance is given by
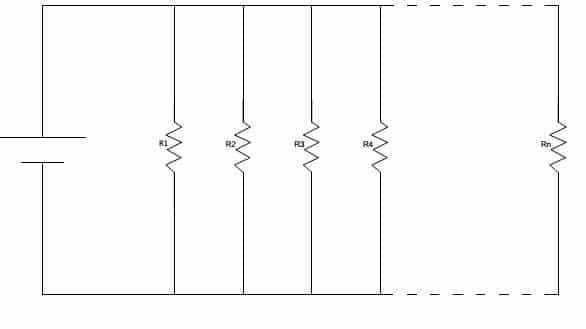
IT = I1 + I2 + I3 + … InV/Req = V/R1 + V/R2+ V/R3 + …..+ V/Rn
Dividing the whole equation by V.,
1/Req = 1/R1 + 1/R2+ 1/R3 + …..+ 1/Rn
From the above equation, it is evident that when a set of resistances are connected in parallel then the reciprocal of equivalent resistance is equal to the sum of reciprocal of individual resistances.
Read more articles like this: